On the Janus Numbers page, you saw how to write Janus numbers and how to do some basic calculations. An abacus makes that easier.

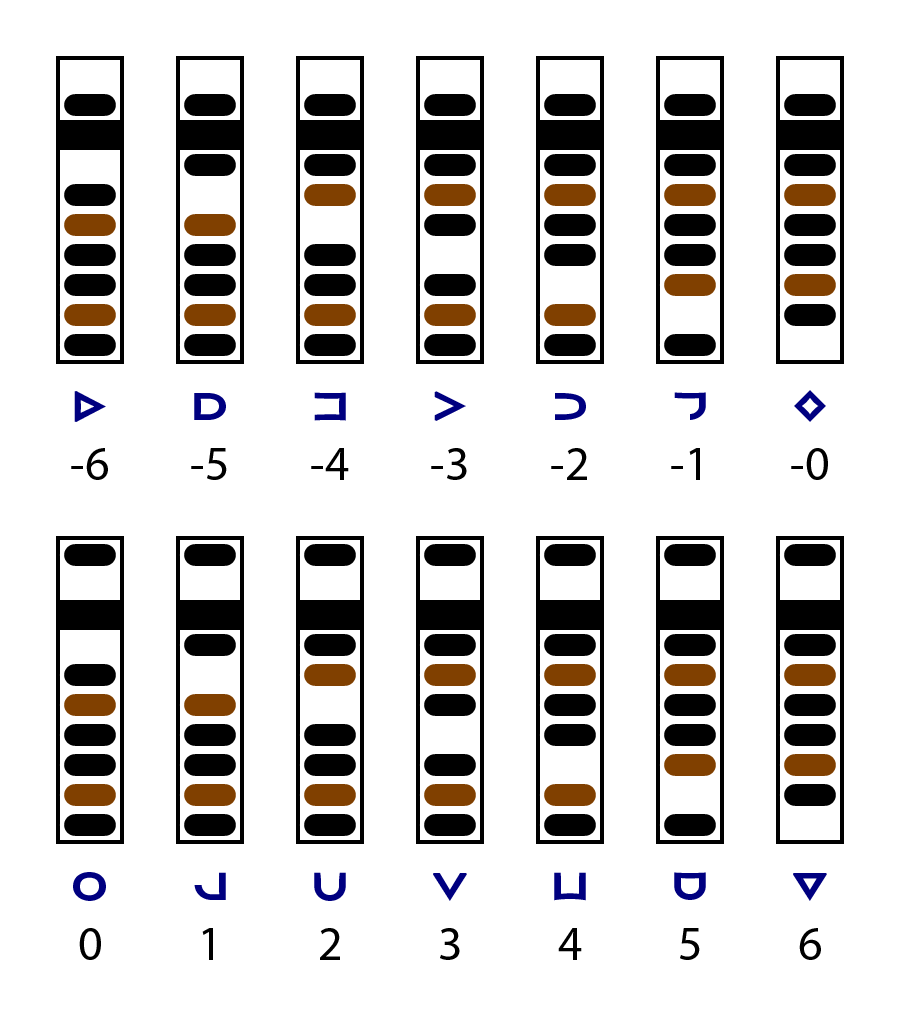
The abacus has a long and interesting history which you can read about elsewhere. Before the invention of mechanical and then electronic calculators, it was the most advanced technology for calculation all over the world, and it is still in use in many places. The Russian abacus has 10 beads per rod, the Chinese has 5 below and 2 above a separating bar, and the Japanese has 4 and 1. The Janus abacus, introduced on this page, has 6 beads below the bar and only 1 above. Here's what one looks like:

Like Western abaci, the Janus abacus has two beads per rod of a different color, to help you see quickly how many beads are up or down. It also offers separators between columns (I use colored elastic bands, the thicker ones used to hold hair). These separators make it easier to put more and longer numbers on the abacus at the same time. For example, operations like multiplication and division involve three numbers, and they're all shown on the abacus. This abacus has 11 columns, but they can have more or as few as 7.

Each column (rod) of an abacus represents one digit. Here's how that works for a Janus abacus:

How to use an Abacus

There are a few small tips that make using an abacus much easier. The first is simply to stop thinking about numbers! Convert your numbers to beads before the calculation, convert the result to a number after the calculation, but in between, don't think about numbers - think about beads! On a Janus abacus, like on all abaci, making a value bigger always involves moving beads up, and making a number smaller always involves moving beads down.

There are also two equivalence operations - "tricks" - that you need to master so that they become so instinctive that they don't distract you.

• The upper bead is worth six lower beads. If you are adding and you run out of lower beads to move up, move the upper bead up (if you can) and move all six lower beads down, then continue. Likewise, if you are subtracting and you run out of lower beads to move down, move the upper bead down (if you can) and move all six lower beads up, then continue.
• One lower bead in the column to the left is worth all six lower beads in your column, plus the upper bead. If you are adding and all your beads are already up, move them all down and move one lower bead up in the column to the left, then continue. Likewise, if you are subtracting and all your beads are already down, move them all up and move one lower bead down in the column to the left, then continue.

In both cases, the phrase "then continue" means that you have to be able to do these two operations without losing track of how many beads you've moved and still need to move. If you're moving five beads up and there's only room for two, then move the two, make some space using one of the two tricks above, then move the remaining three.

Addition

As you use an abacus for addition, in general, if you move beads up on the right, you have to move beads down on the left.

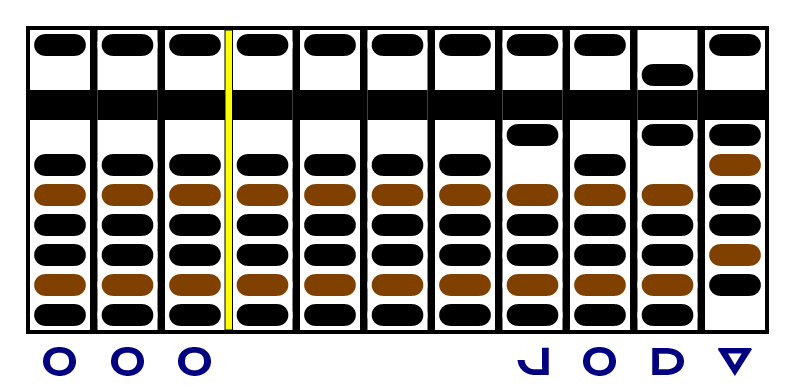
Here's an abacus set up to add 343 (7³) to 1331 (11³). I put the larger addend on the right, but it doesn't really matter. The yellow separator separates the addend on the left from the rest of the abacus.

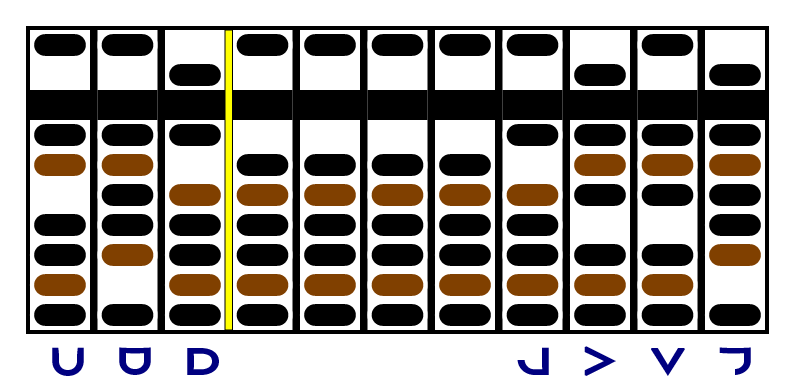
In the first step, we add the  -5 in the units place of the left addend to the  -1 in the units place of the right addend. To do that, we move five beads down (since adding a negative number makes the value smaller) on the right, and we move five beads up on the left. That leaves  -6 in the units place of the right addend, and  0 in the units place of the left addend.

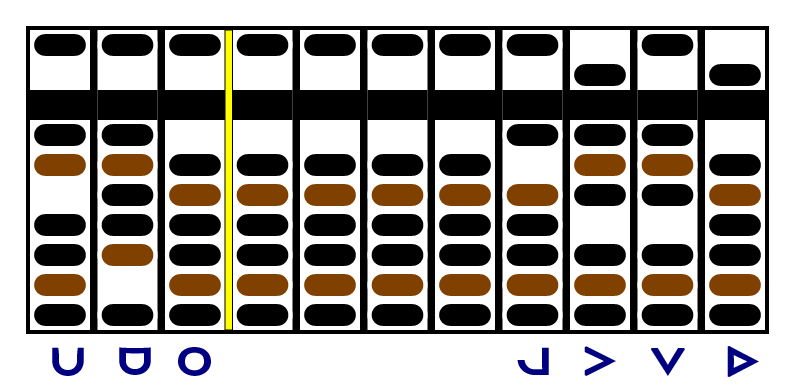
But because these are positive numbers, the sum will be positive, and we don't want it to end with a -6. So we use the second trick to move all the beads up and move one bead down in the next column.

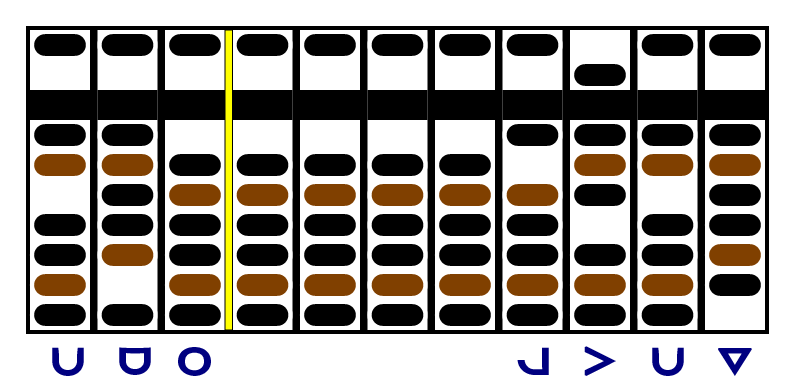
Next, we add the  +5 in the second (dozens) column of the left addend to the  +2 in the second column of the right addend. It doesn't fit - there aren't enough beads! So we move four beads up - that's all that will fit - then use the second trick to move all the beads down and move one up in the next column. Now we can move up the remaining bead back in our second column. We end up with  -5 in the second righthand column, and zero in the second lefthand column.

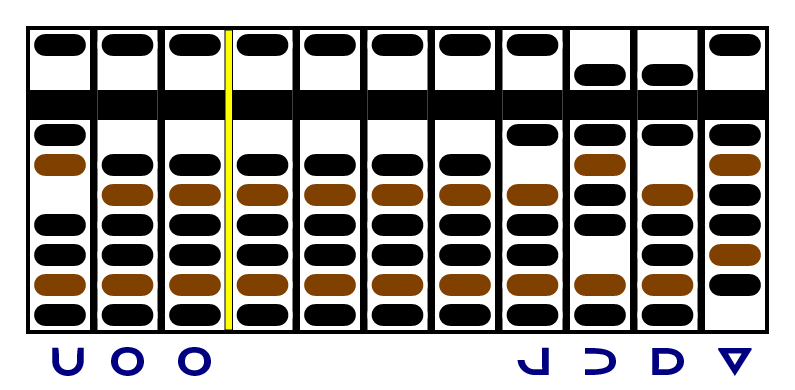
Finally, we add the  +2 in the third column at left to the  -2 in the third column at right. They sum to -0, which we immediately convert to +0 without affecting any other columns. So we're done: the right answer is , or 1674.

Subtraction

As you use an abacus for subtraction, in general, if you move beads down on the right, you have to move beads down on the left. In other words, unlike with addition, in subtraction the two numbers get smaller together.

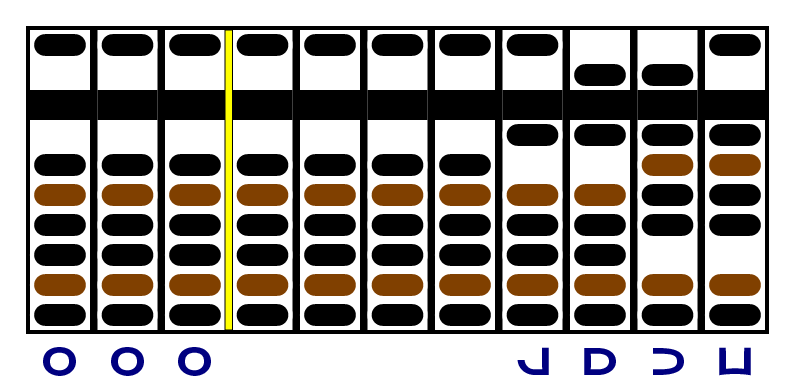
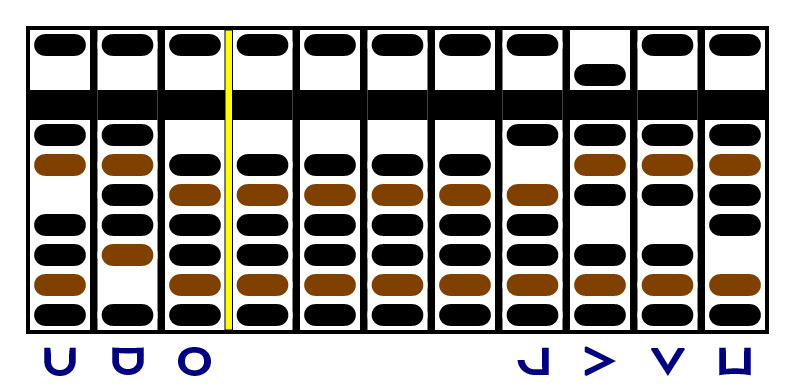
Now let's try a subtraction. In Janus, you could just complement the subtrahend and add the complement to the minuend, but we're going to do a real subtraction: 1331 - 343. So the initial setup is identical:

In the first step, we subtract the  -5 in the units place of the subtrahend from the  -1 in the units place of the minuend. Subtracting -5 is like adding +5, so we end up with  +4.

In the next step, we subtract the  +5 in the subtrahend from the  +3 in the minuend: the result is -2:

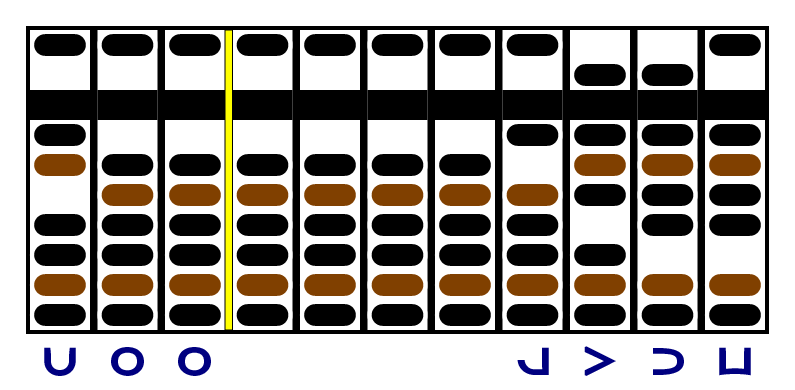
Finally, we subtract the  +2 at left from the  -3 at right, and get  -5. So the answer is , or 988.

Multiplication

Multiplication is a little different. We're going to put all three numbers on the abacus: the smaller multiplicand on the left (I'll call it the "factor") with a separator, then the other multiplicand right after it with another separator, and then we'll build the product on the right. We're going to handle the second multiplicand digit by digit starting from the right, so that every digit we finish adds another place for the product, if needed.

Here's the starting setup for 343 × 1331:

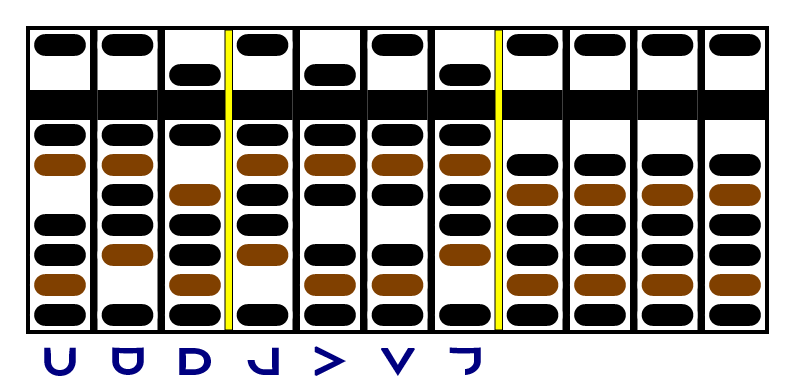
As promised, we're going to start with the  -1 in the units place of the multiplicand. We going to use it to multiply each of the digits in the factor, one at a time, and put the result on the right. In this case, it's easy: we just complement the factor, write it, and then zero the digit we just used.

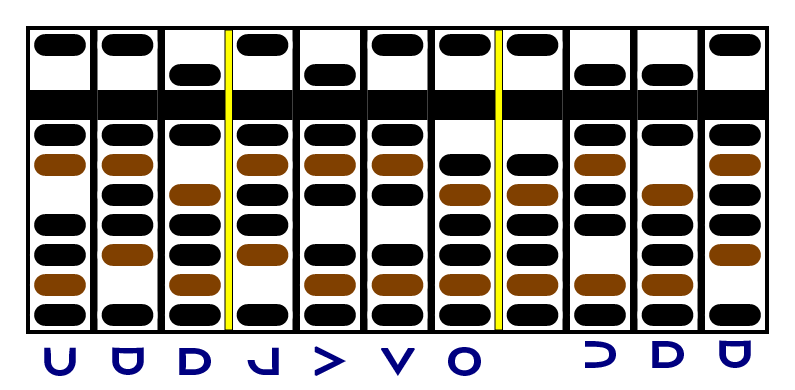
But now we're going to move the separator at the right end of the multiplicand one column to the left, crossing over a zero - and we're also going to add a third separator one column to the left of the units place of the product: the last digit of the product is already determined.

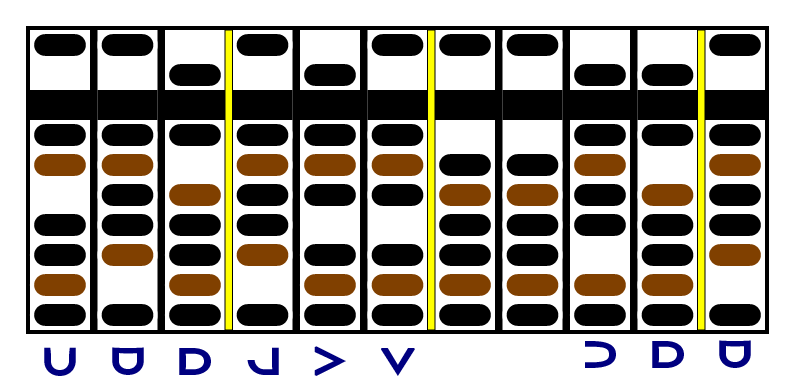
We're going to do the other digits of the multiplicand the same way. First, we multiply the entire factor by the last digit of the multiplicand and add the result just to the left of the separator in the product, one column at a time.  +3 ×  -5 is -15, and we add it to the  -5 at right to get -20, which is . So we put +4 in the last column to the left of the separator in the product, and add -2 in the column to its left. But we're not ready to zero anything.

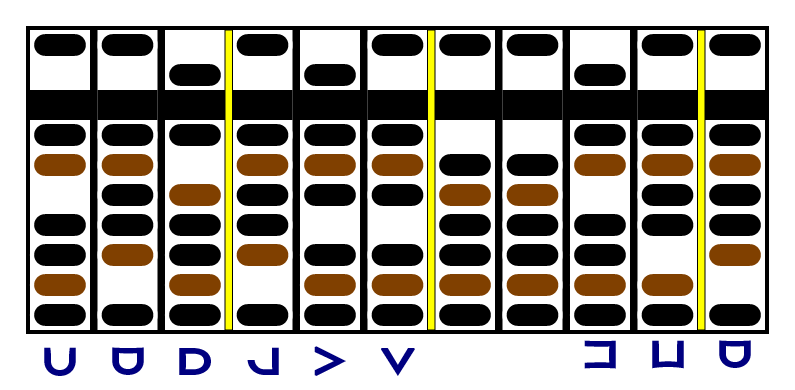
The same digit  +3 × the  +5 in the second column is +15, which is , so we add +3 to the second column to get  -1 and put +1 in the empty column to its left:

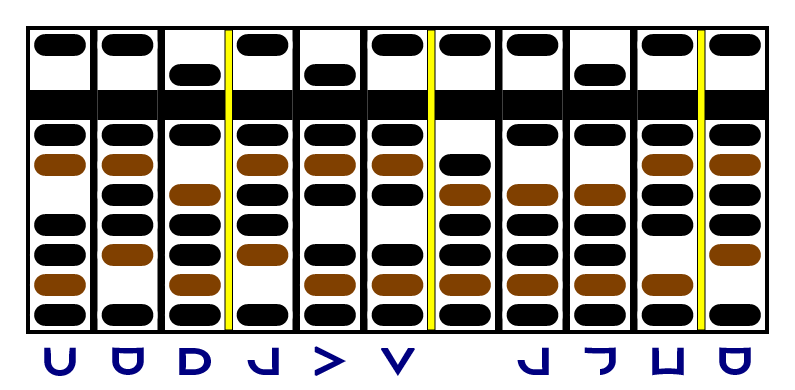
To finish with the  +3 digit, we multiply it by the  +2 in the third column of the factor, and add the result to the third column of the product. Since it doesn't fit, we have to carry it over to the next column. Then we can zero the rightmost column of the multiplicand and move both separators one column left - just in time, since we're running out of columns!

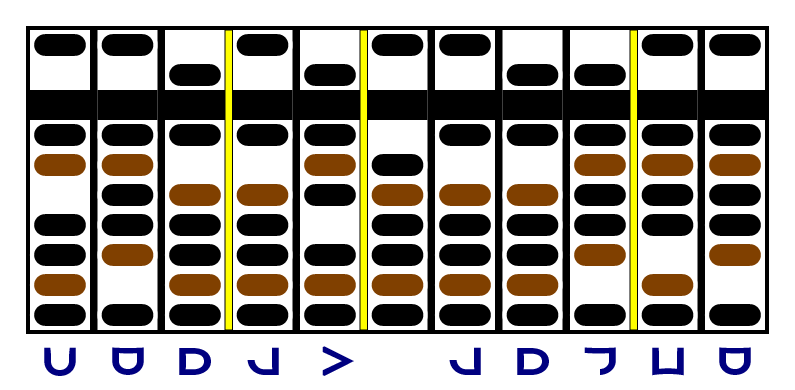
Now we're ready to work on the new rightmost digit of the multiplicand, which is  -3. We multiply it by the three digits of the factor, one at a time from the right, and put the results in the corresponding column of the product, counting from the separators. Once that's done, we zero our digit and move the separators.

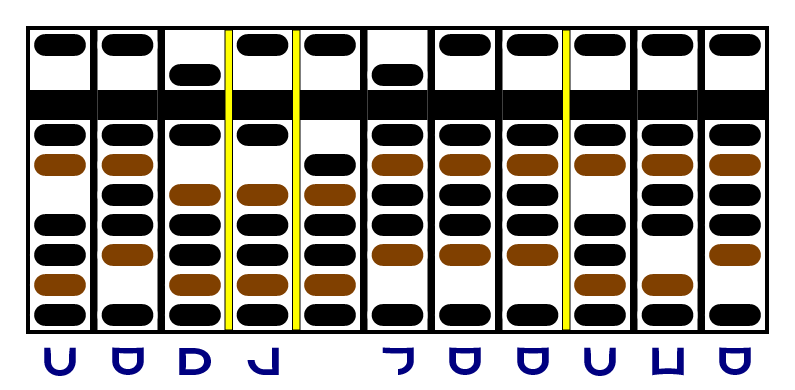
We only have one more digit left in the multiplicand, the  +1. We can just add the digits to the correct columns, matching separators. Once that's done, we zero our last digit and remove the separators: we don't need them any more. The multiplicand has been used up, and the final product is on the right: , or decimal 456533.

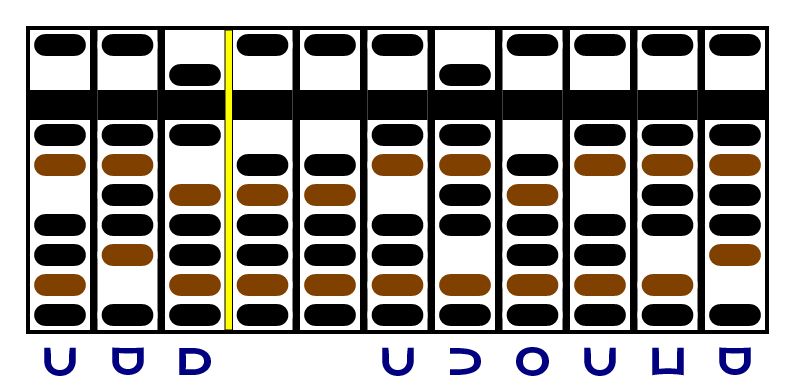
This algorithm is not simple, but it walked us through twelve multiplications of single digits while keeping track of the positions, and it fit a 6-digit result next to 7 digits of input on an 11-column abacus.

Repeated Addition

The problem with the above procedure for multiplication is that you have to think, and when we use an abacus, we want to replace thinking with pushing beads. So I'm going to teach you another way to do multiplication on a Janus abacus: via repeated addition.` The principle is obvious: instead of calculating 3 × 7 = 21, we're going to calculate 7 + 7 + 7 = 21. Since addition is what abaci are good at, and since we only need to add an average of three times per column, this turns out to be pretty efficient.

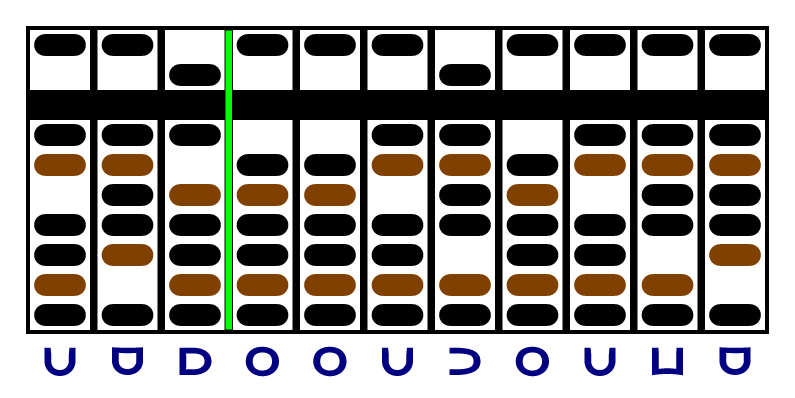
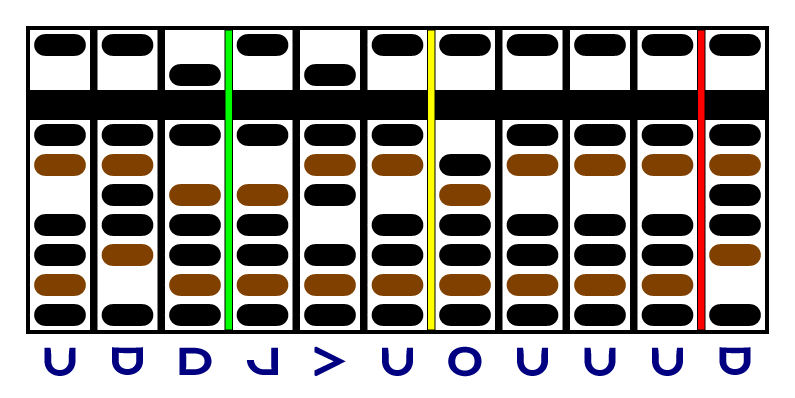
We'll set the abacus up with the "factor" on the left, as usual, delimited by a green separator. This won't change as we calculate. I usually choose the smaller multiplicand as the factor, so I end up doing more but easier additions, but you may have the opposite preference. I put the other multiplicand after it, delimited by a yellow separator, and I zero out the remaining columns to use for the product, with a red separator after them. We'll use the same example as we did above; here's what that looks like:

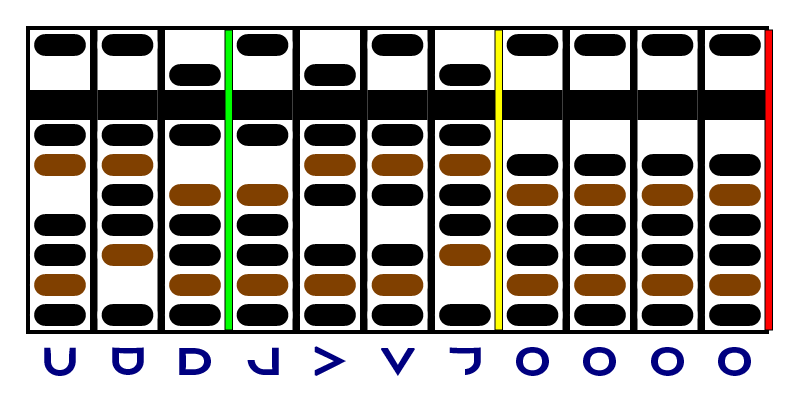
Now we're going to start adding the factor to the product, lining both up at the right. And every time we add the product, we're going to decrement the last column of the multiplicand. But since the last digit of the multiplicand is negative , we have to subtract the factor and increment the multiplicand:

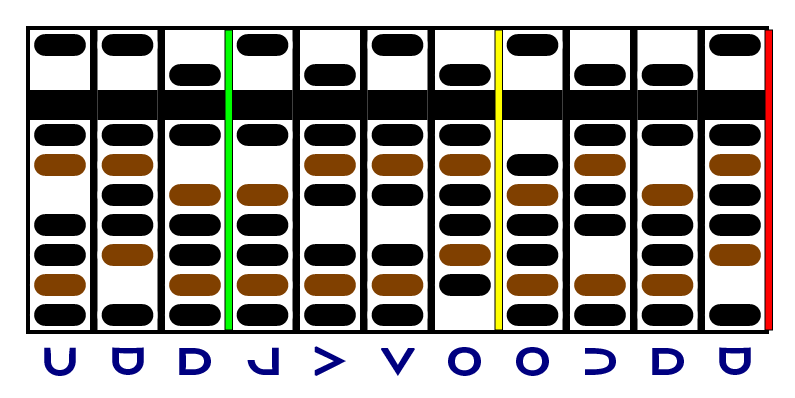
Now, the last column of the multiplicand is a zero, so we're going to move the yellow and red separators one column left and continue, lining the red up with the green. The last digit of the multiplicand is positive, so we're going to add and decrement:

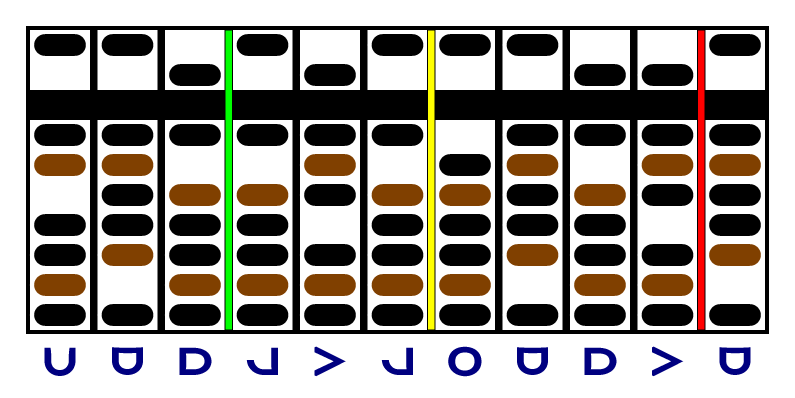
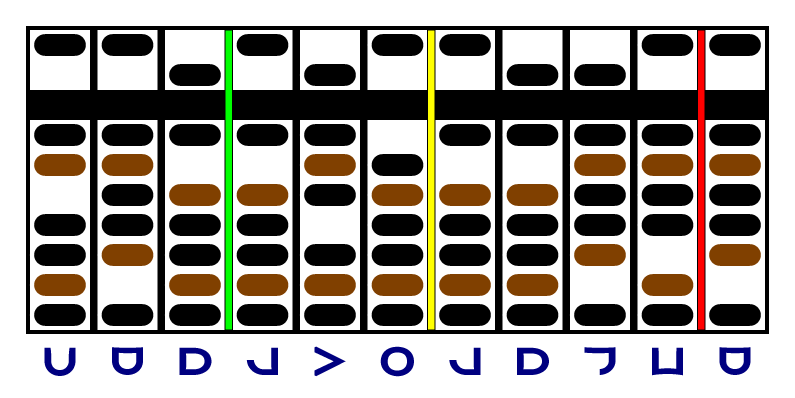
Again, the last column of the multiplicand is a zero, so we move the yellow and red separators and continue. The new last digit of the multiplicand is negative, so we have to subtract and increment:

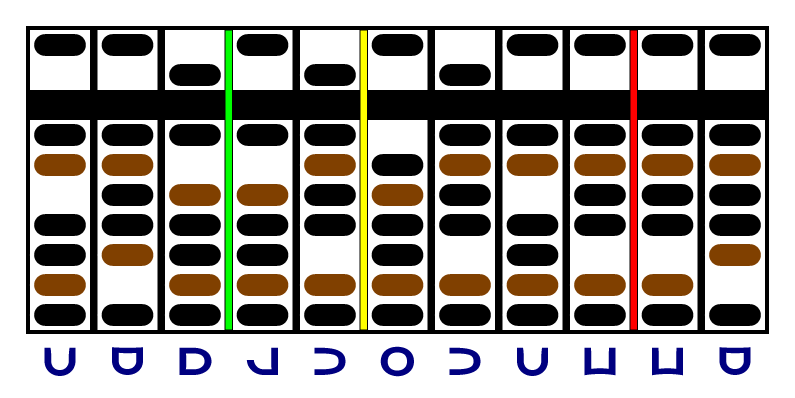
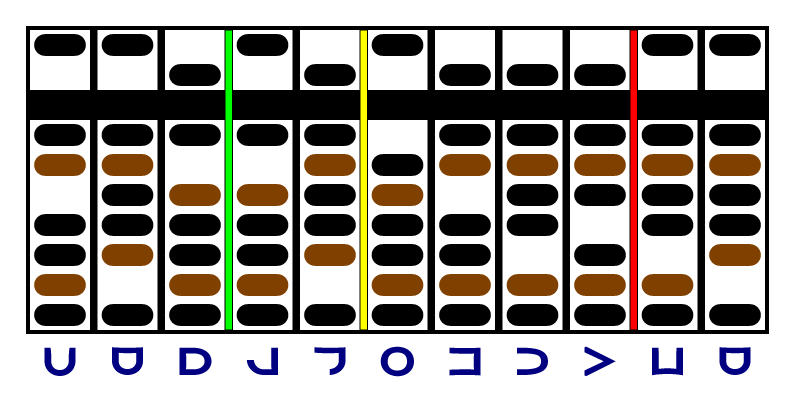
Again, the last column of the multiplicand is a zero, so we move the yellow and red separators and continue. The new last digit of the multiplicand is positive, so we add and decrement:

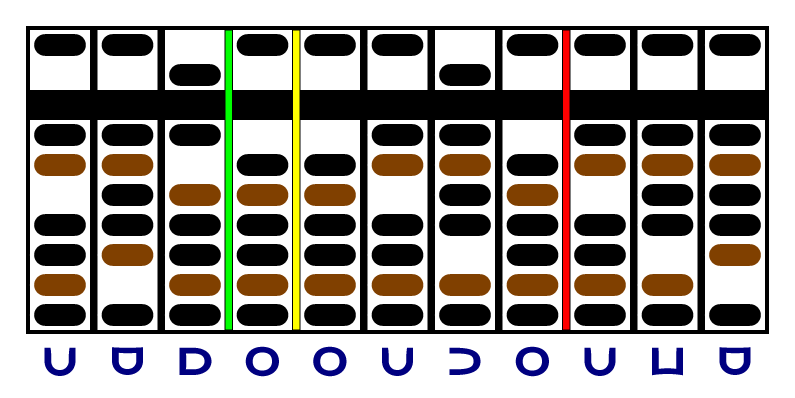
The multiplicand is all zeroes now, so we're done. We don't need the yellow or red separators any more, and the product can be read on the right: , or decimal 456533, the same answer as above.

Division

With division, we move from the realm of integers into the realm of real numbers. The difference between integers and real numbers is that integers are grounded on the right, at the units place, while real numbers are anchored at the left. Even if the dividend is an integer, we convert it to a real number before the calculation. The divisor, in contrast, must be an integer, so we multiply it by the base (10 or 12) until all the significant figures are to the left of the decimal point, then throw away the rest. Then we have to multiply the dividend by the same power, to keep the decimal place where it belongs.

If we were doing traditional long division, whether on paper or on the abacus, we'd repeat the following procedure:

1. Estimate what multiple of the divisor will get closest to the remainder (the dividend, the first time around) without going over it.
2. Write that multiple as the next digit of the quotient.
3. Multiply the divisor by that multiple.
4. Subtract that product from the remainder.
5. If the product is too big or too small, undo those four steps and redo step 1.
6. If not, the difference is the new remainder.
7. When you're happy with the number of digits in the quotient, stop.

To adapt that procedure to Janus numbers, we'd have to amend step 1 to get as close as possible to the remainder whether or not you go over it, and that's a more difficult estimation. But in general, the procedure above is pretty complicated, and it involves an estimation for which the abacus is no help, and a multiplication for which you can't use the abacus even though you'd like to.

So on the Janus abacus, we use a different procedure: repeated subtraction. There's no estimation and no multiplication, so it's much simpler. And since the largest Janus digit is only 6 (not 9), you'll only have to do an average of three subtractions - not too bad. Best of all, with repeated subtraction, you don't have to think very much: just keep subtracting until the first digit of the remainder disappears.

As an example, we're going to calculate how many inches there are in a meter. An inch is defined as 2.54cm, and a meter is 100cm, so we're computing 100/2.54. To convert 2.54 (base 10) to a Janus integer, we simply multiply it by twelve until all the significant figures are left of the decimal - in this case, twice to get 366 - and then convert that to Janus as an integer - : that's the divisor. The dividend 100 is Janus , but we have to multiply it by 12 twice to compensate for the divisor, so our starting dividend is .

To do division on the abacus, the divisor is written on the left, followed by a separator (I used a green one here). The dividend is written on the right. We could put it in the last five columns, since it's a five-digit number, but let's put it two columns left of that to give us a little bit more precision. The quotient goes in between them, with a (yellow) separator on the right. To start, make it only one column wide, but it will have room to get larger as the remainder gets smaller. And let's add one more (red) separator to the right of the first three nonzero digits of the dividend, since that will be our first subtraction.

Here's how the abacus sets up for this operation:

I'll use drawings instead of photos:

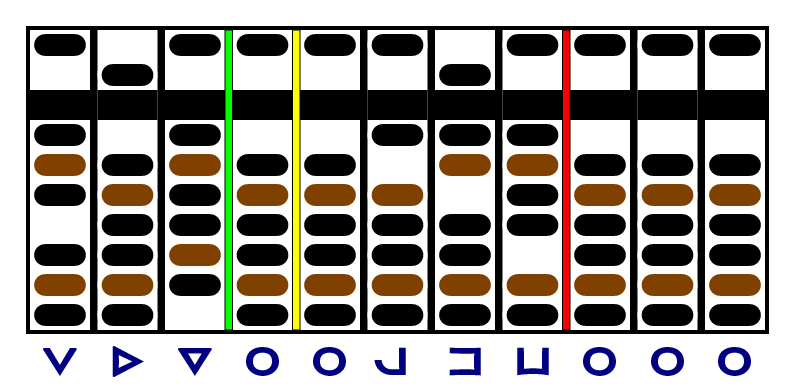
Before we start, let's figure out the magnitude of the quotient. We start by assuming it will be one digit, but we're going to shift the divisor two columns left to subtract it from the first three digits of the dividend, so we add those two digits to the quotient: it will have three digits.

One last item in preparation: we calculate half of the divisor. That's our stop signal: we're going to keep subtracting until we get under that number, even if we end up with a negative number that's closer to zero. Half of  is , and the complement is . We're looking for a remainder that's between those two numbers.

Now let's try to subtract the divisor  from the first three digits of the dividend , mentally lining the green separator up with the red one. In fact, the number spelled by the first three digits of the dividend is already under our limit, so we don't need to subtract any more. We could write a zero in the first column of the quotient and move the yellow separator to the right, but instead we're just going to throw that zero away and reduce the magnitude of the quotient: now it will be only two digits - the third digit was the leading zero we threw away.

So we'll just move the red separator one column right and turn our attention to subtracting  from , starting at the red and green separators and moving left, and then add one to the first digit of the quotient to record the one subtraction. Here's what the abacus looks like after that:

We keep subtracting:

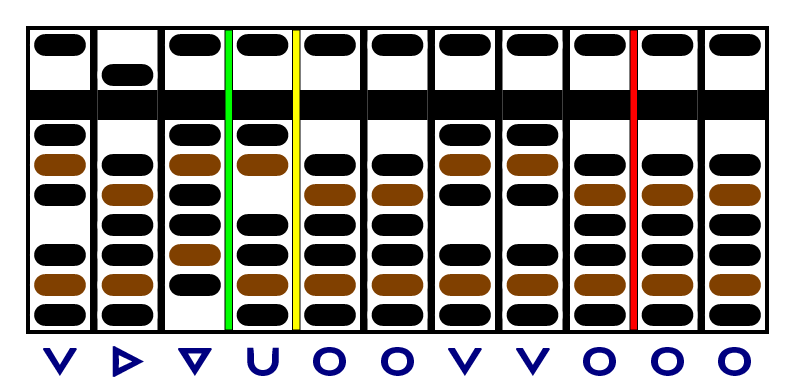
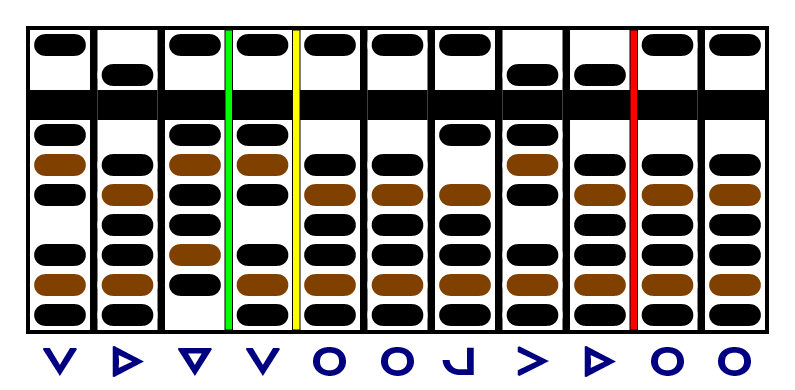
That brought our remainder under the limit, so we'll move both the yellow and red separators to the right and start work on the next digit of the quotient. Here's what it looks like after subtraction:

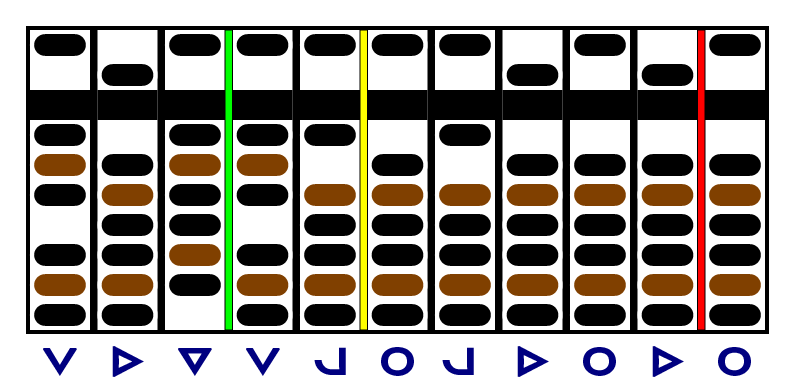
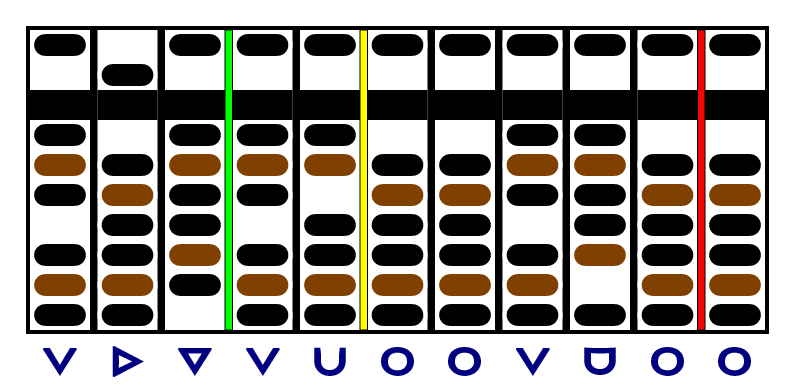
It only took us two subtractions to get a zero in the first column of the remainder, but we keep subtracting:

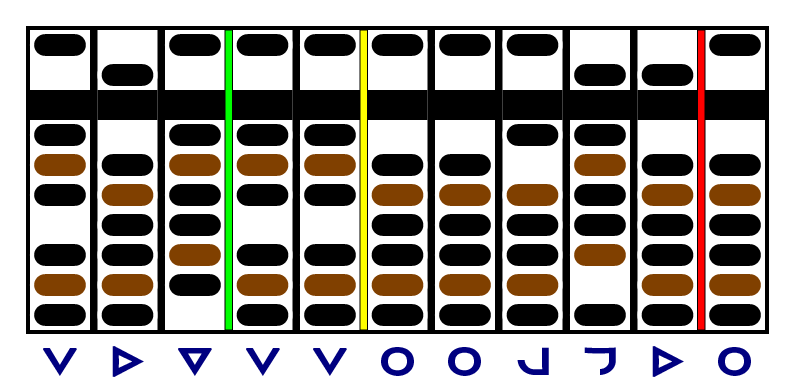
We're already under the limit, so we'll move both the yellow and red separators right and start work on the next digit of the quotient.

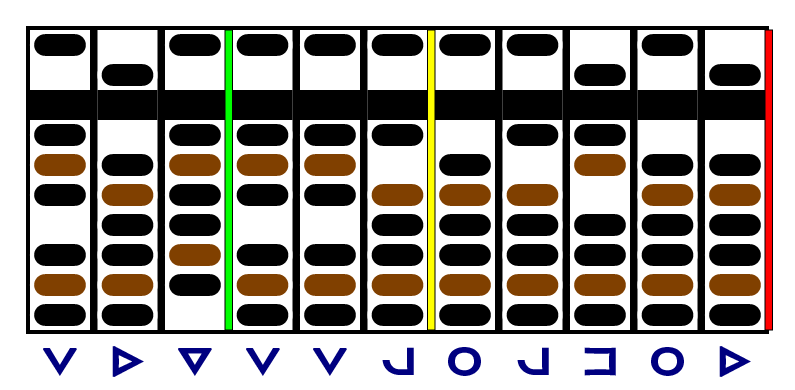
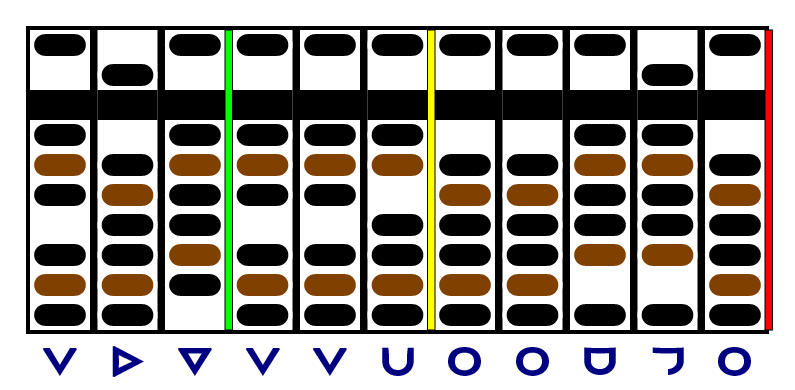
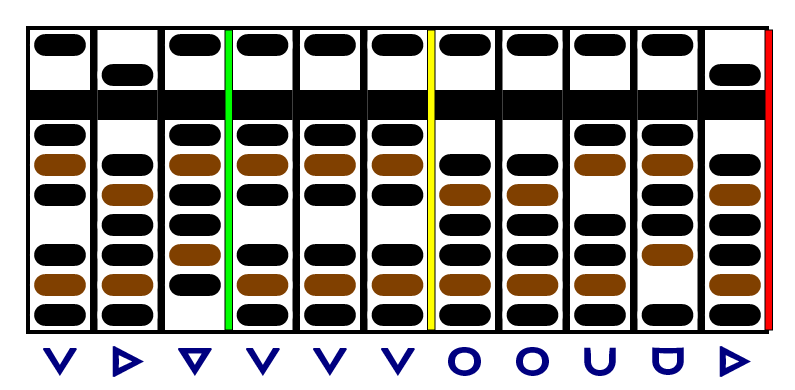
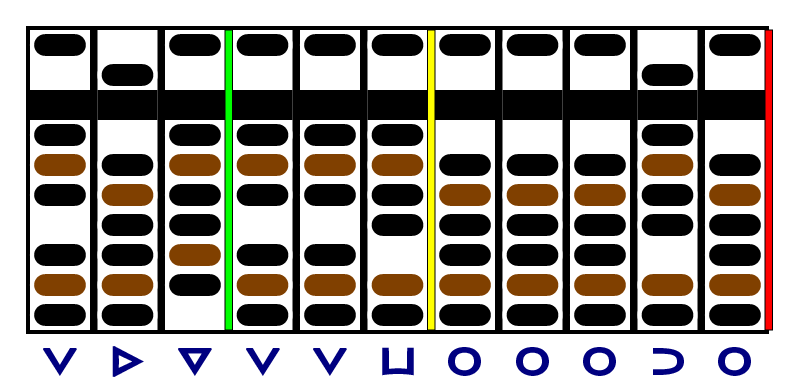
Our remainder is under the limit again, so we should move right. But we already have three digits of quotient - that's all we need. The divisor and dividend have three significant figures, so that's all we can generate in our answer. (Actually, the number of centimeters in an inch is 2.54000000…, and the number of centimeters in a meter is 100.000000…, so we could choose our precision, but we'll stick with three significant figures for this example.)

So that's the answer: . Converting back to decimal, that's 472. And dividing by 12 to get a two-digit quotient, we end up with 39.3 - the correct answer :) Once you get fast on your additions and subtractions, it's pretty straightforward.